¿Que Son?
Los poliedro son elementos geométricos que disponen de caras planas que albergan un volumen que no es infinito. Un poliedro puede ser entendido como un cuerpo solido y tridimensional. Cuando todas sus caras y ángulos son iguales entre si, se le clasifica como un poliedro regular. De lo contrario, sera un poliedro irregular.
Otra clasificación posible esta vinculada a la cantidad de caras que presenta. Un poliedro de seis caras recibe el nombre de hexaedro, un poliedro de cinco lados se conoce pentaedro y así sucesivamente, formado siempre la denominación del prefijo griego correspondiente ( hexa, penta, tetra, etc ).
Por otra parte, se puede diferenciar entre poliedro cóncavos y poliedro convexos. Los poliedros cóncavos son aquellos que, al unir dos puntos situados dentro del cuerpo, el segmento correspondiente sale de la superficie. En cambio, en los poliedro convexos, los segmentos que vinculas dos puntos del espacio interior nunca sale del cuerpo geométrico.
Un ejemplo de poliedro es el cubo, un poliedro regular de cuatro caras iguales, cuyos ángulos interiores son congruentes entre si. Esto quiere decir que los dados construidos de esta manera son poliedros. Las cajas cuyas caras son cuadrados también ingresan dentro del grupo de los poliedros.
Otro ejemplos de poliedros son los prismas, en este caso, se trata de poliedro irregulares. Es importante resaltar que las clasificaciones no siempre son excluyentes. El prisma es un poliedro irregular pero, a su vez, es un poliedro convexo.
Estos son algunos poliedros regulares:
1 Tetraedro
Es una pirámide triangular regular.
Área y volumen del tetraedro
Como un tetraedro está formado por 4 triángulos equilaláteros, podemos hallar el área de un triángulo equilátero y multiplicar por 4 para obtener el área del tetraedro.
2 Hexaedro o cubo
Área y volumen del cubo
3 Octaedro
Área y volumen del octaedro
4 Dodecaedro
Área y volumen del dodecaedro
5 Icosaedro
Área y volumen del icosaedro
Dentro de los poliedros irregulares encontramos el prisma.
Prisma :Un prisma es un poliedro que tienen dos caras paralelas e iguales llamadas bases y sus caras laterales son paralelogramos.
Elementos de un prisma
Altura de un prisma es la distancia entre las bases.
Los lados de las bases constituyen las aristas básicas y los lados de las caras laterales lasaristas laterales, éstas son iguales y paralelas entre sí.
Área lateral de un prisma
Área total de un prisma
Volumen de un prisma
Tipos de prismas
Prismas regulares
Prismas irregulares
Prismas rectos
Prismas oblicuos
Paralelepípedos
Ortoedros
Tipos de prismas según su base
Prisma triangular
Prisma cuadrangular
Prisma pentagonal
Prisma hexagonal
Un ejemplo de como calcular un prisma:
Calcula la altura de un prisma que tiene como área de la base 12 dm2 y 48 l de capacidad.
Los Poliedros tienen todas sus caras planas. Los Prismas y las Pirámides son poliedros, por ejemplo. En los prismas las caras laterales (de los costados) son "paralelogramos" y las bases son "polígonos" paralelos (nunca se tocan, se enfrentan) y congruentes; en las pirámides hay una sola base y un vértice en el que concurren todas sus caras menos una, o sea, la base. Los poliedros y los redondos (cilindros, conos, esferas) entran en la clasificación de los cuerpos geométricos. En la primaria es muy común que en materias como artística y matemática nos hagan representar pirámides, en sí cuerpos geométricos.
Cuerpos Redondos
El cono, el cilindro y la esfera
Estos tres cuerpos se generan al hacer girar una línea alrededor de un eje. La línea que gira recibe el nombre de generatriz y los puntos que ella describe forman una circunferencia.
El cono
Es el cuerpo geométrico redondo que se obtiene al girar una recta oblicua desde un punto fijo del eje. A ese punto se le llamacúspide. La recta, llamada generatriz, gira a lo largo de una circunferencia, directriz, que se encuentra en otro plano.
Otra forma más sencilla de determinar la formación de un cono es decir que se genera al rotar un triángulo rectángulo alrededor de uno de sus catetos.
Elementos de un cono recto
- Eje: es el cateto AC. Alrededor de él gira el triángulo rectángulo.
- Base: es el círculo que genera la rotación del otro cateto, AB. Por lo tanto, AB es el radio del cono. La base se simboliza: O (A, AB)
- Generatriz: es la hipotenusa del triángulo rectángulo, BC, que genera la región lateral conocida como manto del cono.
- Altura: corresponde al eje del cono, porque une el centro del círculo con la cúspide siendo perpendicular a la base.
Observa los elementos del cono recto en este esquema:
El cono tiene una cara basal plana y una cara lateral curva. Posee una arista basal y un vértice llamado cúspide.
Cono recto y cono oblicuo
Si la altura coincide con su eje, el cono es recto. Si el eje y la altura no coinciden, el cono es oblicuo.
Red del cono
Al abrir un cono obtenemos su red, es decir, la plantilla dibujada en un mismo plano para poder construirlo.
La cara lateral o manto de un cono corresponde a un sector circular.
Llamamos sector circular a una parte del círculo formado por 2 radios y el arco de circunferencia comprendido entre ellos.
Llamamos sector circular a una parte del círculo formado por 2 radios y el arco de circunferencia comprendido entre ellos.
En el manto del cono, los radios son la generatriz, y el arco equivale al perímetro de la circunferencia basal.
El cilindro
Este cuerpo redondo se forma con todas las rectas paralelas que cortan a 2 circunferencias congruentes ubicadas en planos paralelos.
Nuevamente obtendremos, de forma más sencilla, la formación de un cilindro recto. Haremos girar un rectángulo alrededor de uno de sus lados.
Elementos de un cilindro recto
- Eje: lado AD, alrededor del cual gira el rectángulo
- Bases: son los círculos paralelos y congruentes que se generan al girar los lados AB y CD del rectángulo. Cada uno de estos lados es el radio de su círculo y también, el radio del cilindro.
- Altura: corresponde al mismo eje AD, es perpendicular a las bases y llega al centro de ellas. Esta es la razón por la que el cilindro es recto.
- Generatriz: es el lado BC, congruente con el lado AD, y que al girar forma la cara lateral o manto del cilindro.
Observa los elementos del cilindro en este esquema:
El cilindro tiene 2 caras basales planas, paralelas y congruentes, 1 cara lateral que es curva y 2 aristas basales.
Red del cilindro
Al abrir un cilindro y colocar todas las caras en un mismo plano, obtenemos su red. Así:
Puedes observar que en esta red se nos forma un rectángulo para la cara lateral, cuyos lados son el perímetro de las circunferencias que forman las bases.
La esfera
Es el cuerpo redondo que se genera al rotar un semicírculo alrededor de su diámetro.
Elementos de una esfera
- Generatriz: es la semicircunferencia que genera la superficie esférica
- Centro de la esfera: es el centro de la semicircunferencia y corresponde al punto O
- Radio de la esfera: es el radio de la semicircunferencia: OA
- Diámetro de la esfera: es el segmento que une 2 puntos opuestos de la superficie esférica, pasando por el centro: AB
Observa los elementos en este esquema:
La esfera tiene una sola cara curva.
Cortes
Una esfera puede ser cortada por un plano que pasa por su centro. De esta forma se obtienen 2 semiesferas y el plano deja como borde un círculo máximo.
Si el plano corta a la esfera sin pasar por su centro se obtienen 2 casquetes esféricos.
Cilindro:
Un rectángulo que gira alrededor de uno de sus lados genera, produce, creaun cilindro:
Un rectángulo que gira alrededor de uno de sus lados genera, produce, creaun cilindro:
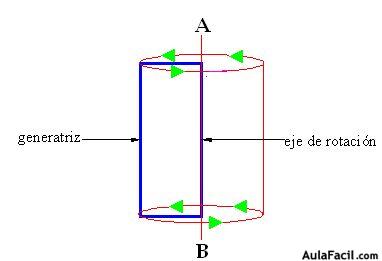
El rectángulo de la figura uno de los lados más largos gira alrededor del eje AB. El lado paralelo, a medida que gira crea o genera un cilindro en la dirección que señalas las flechas de color verde.
Al lado que genera una figura se le llama generatriz.
Al lado que genera una figura se le llama generatriz.
Para hacer un cilindro necesitas dos círculos y un rectángulo cuya longitud equivale a la longitud de la circunferencia de cualquiera de las dos bases:
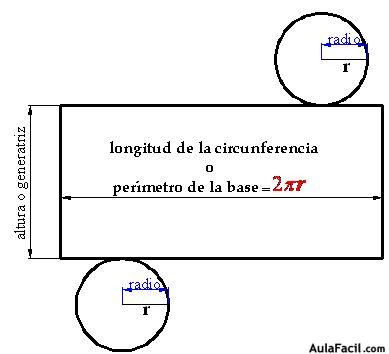
En la figura ves dos círculos de radio r y un rectángulo cuya longitud equivale a la circunferencia que envuelve a uno de los círculos, es decir,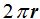 
y la altura es el valor de la generatriz o uno de los lados más largos del rectángulo.
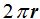y la altura es el valor de la generatriz o uno de los lados más largos del rectángulo.
El área lateral es igual al perímetro de la base (la longitud de la circunferencia) que será la base del rectángulo por lo que mida su altura o la generatriz.
Llamamos P al perímetro
h a la altura o generatriz
Llamamos P al perímetro
h a la altura o generatriz
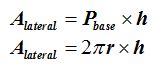
El área total igual al área lateral más el área de las dos bases que son 2 círculos iguales.
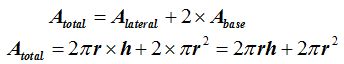
15(4).12 Un cilindro tiene de base un círculo de 2 cm., de radio y una altura de 4 cm. ¿Cuáles son sus áreas lateral y total?
Respuestas: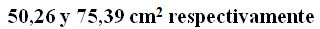 
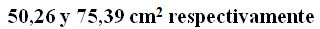
Solución
El área lateral será:
El área lateral será:
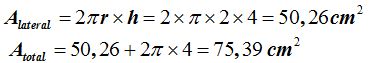
15(4).13 Calcula las áreas lateral y total de un cilindro de 5 cm., como radio de la base y 11 cm., de altura.
Respuestas: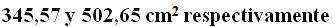 
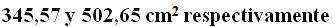
No comments:
Post a Comment